Java背包問題實現(xiàn)

更新時間：2022-04-25 10:36:38 來源：動力節(jié)點瀏覽1251次

1. 簡介

背包問題是一個有很多應(yīng)用的組合優(yōu)化問題。在本Java教程中，動力節(jié)點小編將用 Java 解決這個問題。

2. 背包問題

在背包問題中，我們有一組物品。每個項目都有一個重量和一個價值：

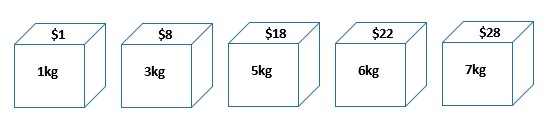
我們想把這些物品裝進背包。但是，它有一個重量限制：

因此，我們需要選擇總重量不超過重量限制的物品，并且它們的總價值盡可能高。例如，上面例子的最佳解決方案是選擇 5kg 的物品和 6kg 的物品，在重量限制內(nèi)，最大值為 40 美元。

背包問題有幾種變化。在本教程中，我們將關(guān)注0-1 背包問題。在 0-1 背包問題中，每個項目要么被選中，要么被拋在后面。我們不能拿走一個項目的部分金額。此外，我們不能多次拿走一個項目。

3. 數(shù)學定義

現(xiàn)在讓我們用數(shù)學符號形式化 0-1 背包問題。給定一組n 個項目和權(quán)重限制W，我們可以將優(yōu)化問題定義為：

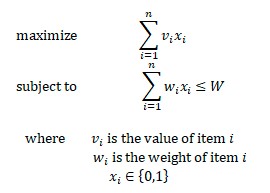
這個問題是 NP 難的。因此，目前還沒有多項式時間算法來解決它。然而，有一個偽多項式時間算法使用動態(tài)規(guī)劃來解決這個問題。

4. 遞歸解決方案

我們可以使用遞歸公式來解決這個問題：

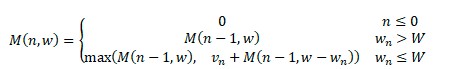
在這個公式中，M(n,w)是重量限制為w的n 個項目的最優(yōu)解。它是以下兩個值中的最大值：

重量限制為w的(n-1)個項目的最優(yōu)解(不包括第n個項目)

第n項的值加上(n-1)項的最優(yōu)解和w減去第n項(包括第n項)的權(quán)重

如果第n個項目的重量超過當前重量限制，我們不包括它。因此，屬于上述兩種情況的第一類。

我們可以在 Java 中實現(xiàn)這個遞歸公式：

int knapsackRec(int[] w, int[] v, int n, int W) {
    if (n <= 0) { 
        return 0; 
    } else if (w[n - 1] > W) {
        return knapsackRec(w, v, n - 1, W);
    } else {
        return Math.max(knapsackRec(w, v, n - 1, W), v[n - 1] 
          + knapsackRec(w, v, n - 1, W - w[n - 1]));
    }
}

在每個遞歸步驟中，我們需要評估兩個次優(yōu)解決方案。因此，此遞歸解的運行時間為O(2 n )。

5. 動態(tài)規(guī)劃方案

動態(tài)規(guī)劃是一種將其他呈指數(shù)級困難的規(guī)劃問題線性化的策略。這個想法是存儲子問題的結(jié)果，以便我們以后不必重新計算它們。

我們也可以用動態(tài)規(guī)劃解決0-1背包問題。為了使用動態(tài)規(guī)劃，我們首先創(chuàng)建一個維度從 0 到n和 0 到W的二維表。然后，我們使用自下而上的方法，用這張表計算最優(yōu)解：

int knapsackDP(int[] w, int[] v, int n, int W) {
    if (n <= 0 || W <= 0) {
        return 0;
    }
    int[][] m = new int[n + 1][W + 1];
    for (int j = 0; j <= W; j++) {
        m[0][j] = 0;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= W; j++) { 
            if (w[i - 1] > j) {
                m[i][j] = m[i - 1][j];
            } else {
                m[i][j] = Math.max(
                  m[i - 1][j], 
                  m[i - 1][j - w[i - 1]] + v[i - 1]);
            }
        }
    }
    return m[n][W];
}

在這個解決方案中，我們對項目編號n和重量限制W有一個嵌套循環(huán)。因此，它的運行時間是O(nW)。