更新時間:2022-12-16 10:28:53 來源:動力節點 瀏覽1390次
遞歸算法時間復雜度的分析,小編來舉例說明。大家來看一下這道面試題:求x的n次方
大家想一下這么簡單的一道題目代碼應該如何寫。
最直觀的方式應該就是,一個for循環求出結果,代碼如下
int function1(int x, int n) {
int result = 1; // 注意 任何數的0次方等于1
for (int i = 0; i < n; i++) {
result = result * x;
}
return result;
}
時間復雜度為O(n)
此時面試官會說,有沒有效率更好的算法呢。
如果同學們此時沒有思路,建議不要說:我不會,我不知道。可以和面試官探討一下,問:可不可以給點提示。
面試官一般會提示:考慮一下遞歸算法
有的同學就寫出了如下這樣的一個遞歸的算法,使用遞歸解決了這個問題
int function2(int x, int n) {
if (n == 0) {
return 1; // return 1 同樣是因為0次方是等于1的
}
return function2(x, n - 1) * x;
}
面試官問:那么這份代碼的時間復雜度是多少?
有的同學可能一看到遞歸就想到了logn,其實并不是這樣
遞歸算法的時間復雜度本質上是要看: 遞歸的次數 * 每次遞歸中的操作次數
那我們再來看代碼,我們遞歸了幾次呢。
每次n-1,遞歸了n次 時間復雜度是O(n),每次進行了一個乘法操作,乘法操作的時間復雜度一個常數項O(1)
所以這份代碼的時間復雜度是 n * 1 = O(n)
這個時間復雜度可能就沒有達到面試官的預期。
于是同學又寫出了這樣的一個遞歸的算法的代碼如下 ,來求 x的n次方
int function3(int x, int n) {
if (n == 0) {
return 1;
}
if (n % 2 == 1) {
return function3(x, n/2) * function3(x, n/2)*x;
}
return function3(x, n/2) * function3(x, n/2);
}
面試官看到后微微一笑,問這份代碼的時間復雜度又是多少呢?
我們來分析一下
首先看遞歸了多少次呢,可以把遞歸的次數 抽象出一顆滿二叉樹。
我們剛剛寫的這個算法,可以用一顆滿二叉樹來表示(為了方便表示 我選擇n為偶數),如圖:
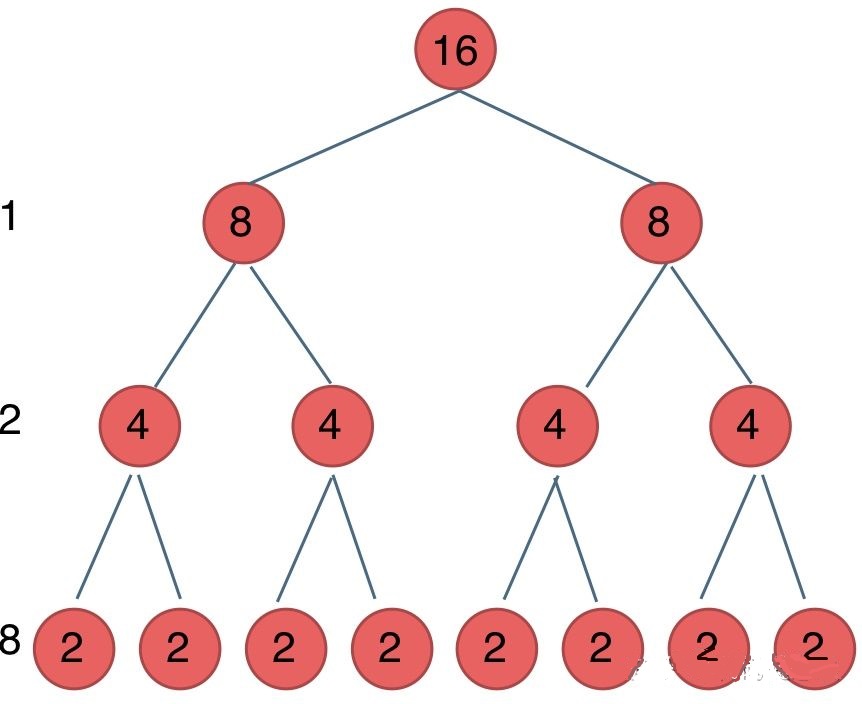
當前這顆二叉樹就是求x的n次方,n為16的情況
n為16的時候 我們進行了多少次乘法運算呢
這棵樹上每一個節點就代表著一次遞歸并進行了一次相乘操作
所以 進行了多少次遞歸的話,就是看這棵樹上有多少個節點。
熟悉二叉樹的同學應該知道如何求滿二叉樹節點數量
這顆滿二叉樹的節點數量就是2^3 + 2^2 + 2^1 + 2^0 = 15
有同學就會發現 這其實是等比數列的求和公式, 如果不理解的同學可以直接記下來這個結論。
這個結論在二叉樹相關的面試題里也經常出現。
這么如果是求x的n次方,這個遞歸樹有多少個節點呢,如下圖所示
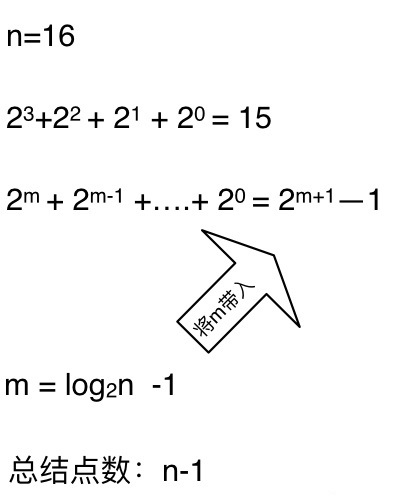
時間復雜度忽略掉常數項-1之后,我們發現這個遞歸算法的時間復雜度依然是O(n)。
此時面試官就會問, 貌似這個遞歸的算法依然還是O(n)啊, 很明顯沒有達到面試官的預期
那么在思考一下 O(logn)的遞歸算法應該怎么寫
這里在提示一下 上面剛剛給出的那份遞歸算法的代碼,是不是有哪里比較冗余呢。
來看這份優化后的遞歸算法代碼
int function4(int x, int n) {
if (n == 0) {
return 1;
}
int t = function4(x, n/2);// 這里相對于function3,是把這個遞歸操作抽取出來
if (n % 2 == 1) {
return t*t*x;
}
return t*t;
}
那我們看一下 時間復雜度是多少
依然還是看他遞歸了多少次
我們可以看到 這里僅僅有一個遞歸調用,且每次都是 n/2
所以這里我們一共調用了 log以2為底n的對數次
每次遞歸了做都是一次乘法操作,這也是一個常數項的操作,
所以說這個遞歸算法的時間復雜度才是真正的O(logn)。
以上就是關于“遞歸算法時間復雜度的分析”介紹,大家如果對此比較感興趣,想了解更多相關知識,不妨來關注一下本站的Java算法視頻教程,里面的課程內容細致全面,通俗易懂,很適合沒有基礎的小伙伴學習,希望對大家能夠有所幫助。
 Java實驗班
Java實驗班
0基礎 0學費 15天面授
 Java就業班
Java就業班
有基礎 直達就業
 Java夜校直播班
Java夜校直播班
業余時間 高薪轉行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構師班
Java架構師班
工作3~5年,晉升架構
提交申請后,顧問老師會電話與您溝通安排學習