B+樹索引是B+樹在數(shù)據(jù)庫中的一種實(shí)現(xiàn)，是最常見也是數(shù)據(jù)庫中使用最為頻繁的一種索引。B+樹中的B代表平衡（balance），而不是二叉（binary），因?yàn)锽+樹是從最早的平衡二叉樹演化而來的。在講B+樹之前必須先了解二叉查找樹、平衡二叉樹（AVLTree）和平衡多路查找樹（B-Tree），B+樹即由這些樹逐步優(yōu)化而來。

二叉查找樹

二叉樹具有以下性質(zhì)：左子樹的鍵值小于根的鍵值，右子樹的鍵值大于根的鍵值。

如下圖所示就是一棵二叉查找樹，

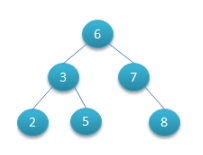
對該二叉樹的節(jié)點(diǎn)進(jìn)行查找發(fā)現(xiàn)深度為1的節(jié)點(diǎn)的查找次數(shù)為1，深度為2的查找次數(shù)為2，深度為n的節(jié)點(diǎn)的查找次數(shù)為n，因此其平均查找次數(shù)為 (1+2+2+3+3+3) / 6 = 2.3次

二叉查找樹可以任意地構(gòu)造，同樣是2,3,5,6,7,8這六個(gè)數(shù)字，也可以按照下圖的方式來構(gòu)造：

但是這棵二叉樹的查詢效率就低了。因此若想二叉樹的查詢效率盡可能高，需要這棵二叉樹是平衡的，從而引出新的定義——平衡二叉樹，或稱AVL樹。

平衡二叉樹（AVL Tree）

平衡二叉樹（AVL樹）在符合二叉查找樹的條件下，還滿足任何節(jié)點(diǎn)的兩個(gè)子樹的高度最大差為1。下面的兩張圖片，左邊是AVL樹，它的任何節(jié)點(diǎn)的兩個(gè)子樹的高度差<=1；右邊的不是AVL樹，其根節(jié)點(diǎn)的左子樹高度為3，而右子樹高度為1；

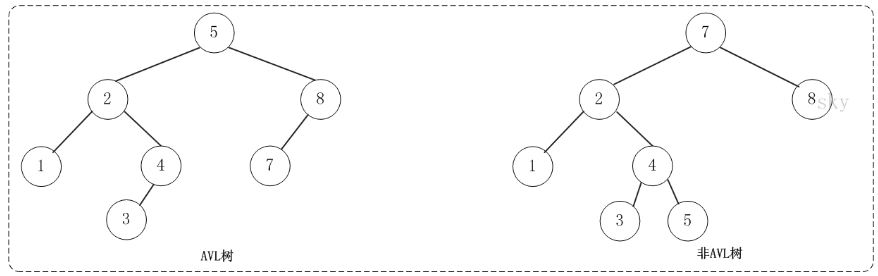
如果在AVL樹中進(jìn)行插入或刪除節(jié)點(diǎn)，可能導(dǎo)致AVL樹失去平衡，這種失去平衡的二叉樹可以概括為四種姿態(tài)：LL（左左）、RR（右右）、LR（左右）、RL（右左）。它們的示意圖如下：

這四種失去平衡的姿態(tài)都有各自的定義：

LL：LeftLeft，也稱“左左”。插入或刪除一個(gè)節(jié)點(diǎn)后，根節(jié)點(diǎn)的左孩子（Left Child）的左孩子（Left Child）還有非空節(jié)點(diǎn)，導(dǎo)致根節(jié)點(diǎn)的左子樹高度比右子樹高度高2，AVL樹失去平衡。

RR：RightRight，也稱“右右”。插入或刪除一個(gè)節(jié)點(diǎn)后，根節(jié)點(diǎn)的右孩子（Right Child）的右孩子（Right Child）還有非空節(jié)點(diǎn)，導(dǎo)致根節(jié)點(diǎn)的右子樹高度比左子樹高度高2，AVL樹失去平衡。

LR：LeftRight，也稱“左右”。插入或刪除一個(gè)節(jié)點(diǎn)后，根節(jié)點(diǎn)的左孩子（Left Child）的右孩子（Right Child）還有非空節(jié)點(diǎn)，導(dǎo)致根節(jié)點(diǎn)的左子樹高度比右子樹高度高2，AVL樹失去平衡。

RL：RightLeft，也稱“右左”。插入或刪除一個(gè)節(jié)點(diǎn)后，根節(jié)點(diǎn)的右孩子（Right Child）的左孩子（Left Child）還有非空節(jié)點(diǎn)，導(dǎo)致根節(jié)點(diǎn)的右子樹高度比左子樹高度高2，AVL樹失去平衡。

AVL樹失去平衡之后，可以通過旋轉(zhuǎn)使其恢復(fù)平衡。下面分別介紹四種失去平衡的情況下對應(yīng)的旋轉(zhuǎn)方法。

LL的旋轉(zhuǎn)。LL失去平衡的情況下，可以通過一次旋轉(zhuǎn)讓AVL樹恢復(fù)平衡。步驟如下：

• 將根節(jié)點(diǎn)的左孩子作為新根節(jié)點(diǎn)。
• 將新根節(jié)點(diǎn)的右孩子作為原根節(jié)點(diǎn)的左孩子。
• 將原根節(jié)點(diǎn)作為新根節(jié)點(diǎn)的右孩子。

LL旋轉(zhuǎn)示意圖如下：

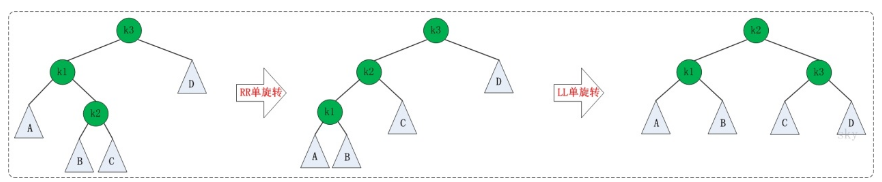
RR的旋轉(zhuǎn)：RR失去平衡的情況下，旋轉(zhuǎn)方法與LL旋轉(zhuǎn)對稱，步驟如下：

• 將根節(jié)點(diǎn)的右孩子作為新根節(jié)點(diǎn)。
• 將新根節(jié)點(diǎn)的左孩子作為原根節(jié)點(diǎn)的右孩子。
• 將原根節(jié)點(diǎn)作為新根節(jié)點(diǎn)的左孩子。

RR旋轉(zhuǎn)示意圖如下：

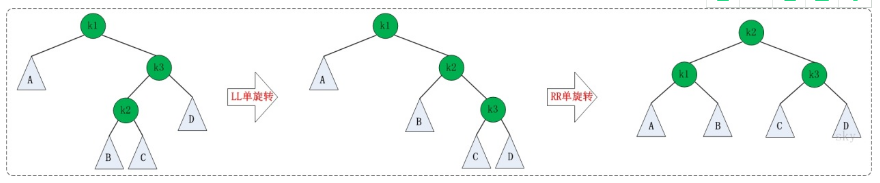
LR的旋轉(zhuǎn)：LR失去平衡的情況下，需要進(jìn)行兩次旋轉(zhuǎn)，步驟如下：

• 圍繞根節(jié)點(diǎn)的左孩子進(jìn)行RR旋轉(zhuǎn)。
• 圍繞根節(jié)點(diǎn)進(jìn)行LL旋轉(zhuǎn)。

LR的旋轉(zhuǎn)示意圖如下：

RL的旋轉(zhuǎn)：RL失去平衡的情況下也需要進(jìn)行兩次旋轉(zhuǎn)，旋轉(zhuǎn)方法與LR旋轉(zhuǎn)對稱，步驟如下：

• 圍繞根節(jié)點(diǎn)的右孩子進(jìn)行LL旋轉(zhuǎn)。
• 圍繞根節(jié)點(diǎn)進(jìn)行RR旋轉(zhuǎn)。

RL的旋轉(zhuǎn)示意圖如下：

平衡多路查找樹（B-Tree）

B-Tree是為磁盤等外存儲(chǔ)設(shè)備設(shè)計(jì)的一種平衡查找樹。因此在講B-Tree之前先了解下磁盤的相關(guān)知識(shí)。

系統(tǒng)從磁盤讀取數(shù)據(jù)到內(nèi)存時(shí)是以磁盤塊（block）為基本單位的，位于同一個(gè)磁盤塊中的數(shù)據(jù)會(huì)被一次性讀取出來，而不是需要什么取什么。

InnoDB存儲(chǔ)引擎中有頁（Page）的概念，頁是其磁盤管理的最小單位。InnoDB存儲(chǔ)引擎中默認(rèn)每個(gè)頁的大小為16KB，可通過參數(shù)innodb_page_size將頁的大小設(shè)置為4K、8K、16K，在MySQL中可通過如下命令查看頁的大?。?/p>

mysql> show variables like 'innodb_page_size';

而系統(tǒng)一個(gè)磁盤塊的存儲(chǔ)空間往往沒有這么大，因此InnoDB每次申請磁盤空間時(shí)都會(huì)是若干地址連續(xù)磁盤塊來達(dá)到頁的大小16KB。InnoDB在把磁盤數(shù)據(jù)讀入到磁盤時(shí)會(huì)以頁為基本單位，在查詢數(shù)據(jù)時(shí)如果一個(gè)頁中的每條數(shù)據(jù)都能有助于定位數(shù)據(jù)記錄的位置，這將會(huì)減少磁盤I/O次數(shù)，提高查詢效率。

B-Tree結(jié)構(gòu)的數(shù)據(jù)可以讓系統(tǒng)高效的找到數(shù)據(jù)所在的磁盤塊。為了描述B-Tree，首先定義一條記錄為一個(gè)二元組[key,data]，key為記錄的鍵值，對應(yīng)表中的主鍵值，data為一行記錄中除主鍵外的數(shù)據(jù)。對于不同的記錄，key值互不相同。

一棵m階的B-Tree有如下特性：

1.每個(gè)節(jié)點(diǎn)最多有m個(gè)孩子。

2.除了根節(jié)點(diǎn)和葉子節(jié)點(diǎn)外，其它每個(gè)節(jié)點(diǎn)至少有Ceil(m/2)個(gè)孩子。

3.若根節(jié)點(diǎn)不是葉子節(jié)點(diǎn)，則至少有2個(gè)孩子

4.所有葉子節(jié)點(diǎn)都在同一層，且不包含其它關(guān)鍵字信息

5.每個(gè)非終端節(jié)點(diǎn)包含n個(gè)關(guān)鍵字信息（P0,P1,…Pn,k1,…kn）

6.關(guān)鍵字的個(gè)數(shù)n滿足：ceil(m/2)-1<=n<=m-1

7.ki(i=1,…n)為關(guān)鍵字，且關(guān)鍵字升序排序。

8.Pi(i=1,…n)為指向子樹根節(jié)點(diǎn)的指針。P(i-1)指向的子樹的所有節(jié)點(diǎn)關(guān)鍵字均小于ki，但都大于k(i-1)

B-Tree中的每個(gè)節(jié)點(diǎn)根據(jù)實(shí)際情況可以包含大量的關(guān)鍵字信息和分支，如下圖所示為一個(gè)3階的B-Tree：

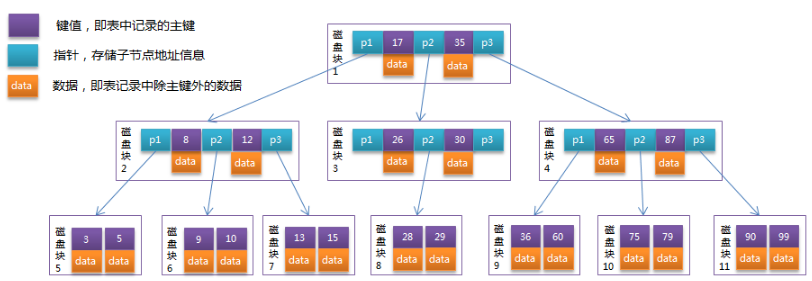
每個(gè)節(jié)點(diǎn)占用一個(gè)盤塊的磁盤空間，一個(gè)節(jié)點(diǎn)上有兩個(gè)升序排序的關(guān)鍵字和三個(gè)指向子樹根節(jié)點(diǎn)的指針，指針存儲(chǔ)的是子節(jié)點(diǎn)所在磁盤塊的地址。兩個(gè)關(guān)鍵詞劃分成的三個(gè)范圍域?qū)?yīng)三個(gè)指針指向的子樹的數(shù)據(jù)的范圍域。以根節(jié)點(diǎn)為例，關(guān)鍵字為17和35，P1指針指向的子樹的數(shù)據(jù)范圍為小于17，P2指針指向的子樹的數(shù)據(jù)范圍為17~35，P3指針指向的子樹的數(shù)據(jù)范圍為大于35。

模擬查找關(guān)鍵字29的過程：

• 根據(jù)根節(jié)點(diǎn)找到磁盤塊1，讀入內(nèi)存?！敬疟PI/O操作第1次】
• 比較關(guān)鍵字29在區(qū)間（17,35），找到磁盤塊1的指針P2。
• 根據(jù)P2指針找到磁盤塊3，讀入內(nèi)存?！敬疟PI/O操作第2次】
• 比較關(guān)鍵字29在區(qū)間（26,30），找到磁盤塊3的指針P2。
• 根據(jù)P2指針找到磁盤塊8，讀入內(nèi)存?！敬疟PI/O操作第3次】
• 在磁盤塊8中的關(guān)鍵字列表中找到關(guān)鍵字29。

分析上面過程，發(fā)現(xiàn)需要3次磁盤I/O操作，和3次內(nèi)存查找操作。由于內(nèi)存中的關(guān)鍵字是一個(gè)有序表結(jié)構(gòu)，可以利用二分法查找提高效率。而3次磁盤I/O操作是影響整個(gè)B-Tree查找效率的決定因素。B-Tree相對于AVLTree縮減了節(jié)點(diǎn)個(gè)數(shù)，使每次磁盤I/O取到內(nèi)存的數(shù)據(jù)都發(fā)揮了作用，從而提高了查詢效率。

B+Tree

B+Tree是在B-Tree基礎(chǔ)上的一種優(yōu)化，使其更適合實(shí)現(xiàn)外存儲(chǔ)索引結(jié)構(gòu)，InnoDB存儲(chǔ)引擎就是用B+Tree實(shí)現(xiàn)其索引結(jié)構(gòu)。

從上一節(jié)中的B-Tree結(jié)構(gòu)圖中可以看到每個(gè)節(jié)點(diǎn)中不僅包含數(shù)據(jù)的key值，還有data值。而每一個(gè)頁的存儲(chǔ)空間是有限的，如果data數(shù)據(jù)較大時(shí)將會(huì)導(dǎo)致每個(gè)節(jié)點(diǎn)（即一個(gè)頁）能存儲(chǔ)的key的數(shù)量很小，當(dāng)存儲(chǔ)的數(shù)據(jù)量很大時(shí)同樣會(huì)導(dǎo)致B-Tree的深度較大，增大查詢時(shí)的磁盤I/O次數(shù)，進(jìn)而影響查詢效率。在B+Tree中，所有數(shù)據(jù)記錄節(jié)點(diǎn)都是按照鍵值大小順序存放在同一層的葉子節(jié)點(diǎn)上，而非葉子節(jié)點(diǎn)上只存儲(chǔ)key值信息，這樣可以大大加大每個(gè)節(jié)點(diǎn)存儲(chǔ)的key值數(shù)量，降低B+Tree的高度。

B+Tree相對于B-Tree有幾點(diǎn)不同：

• 非葉子節(jié)點(diǎn)只存儲(chǔ)鍵值信息。
• 所有葉子節(jié)點(diǎn)之間都有一個(gè)鏈指針。
• 數(shù)據(jù)記錄都存放在葉子節(jié)點(diǎn)中。

將上一節(jié)中的B-Tree優(yōu)化，由于B+Tree的非葉子節(jié)點(diǎn)只存儲(chǔ)鍵值信息，假設(shè)每個(gè)磁盤塊能存儲(chǔ)4個(gè)鍵值及指針信息，則變成B+Tree后其結(jié)構(gòu)如下圖所示：

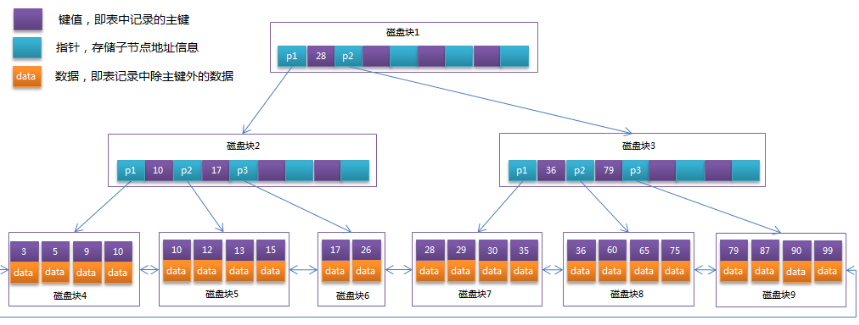
通常在B+Tree上有兩個(gè)頭指針，一個(gè)指向根節(jié)點(diǎn)，另一個(gè)指向關(guān)鍵字最小的葉子節(jié)點(diǎn)，而且所有葉子節(jié)點(diǎn)（即數(shù)據(jù)節(jié)點(diǎn)）之間是一種鏈?zhǔn)江h(huán)結(jié)構(gòu)。因此可以對B+Tree進(jìn)行兩種查找運(yùn)算：一種是對于主鍵的范圍查找和分頁查找，另一種是從根節(jié)點(diǎn)開始，進(jìn)行隨機(jī)查找。

可能上面例子中只有22條數(shù)據(jù)記錄，看不出B+Tree的優(yōu)點(diǎn)，下面做一個(gè)推算：

InnoDB存儲(chǔ)引擎中頁的大小為16KB，一般表的主鍵類型為INT（占用4個(gè)字節(jié)）或BIGINT（占用8個(gè)字節(jié)），指針類型也一般為4或8個(gè)字節(jié)，也就是說一個(gè)頁（B+Tree中的一個(gè)節(jié)點(diǎn)）中大概存儲(chǔ)16KB/(8B+8B)=1K個(gè)鍵值（因?yàn)槭枪乐?，為方便?jì)算，這里的K取值為〖10〗^3）。也就是說一個(gè)深度為3的B+Tree索引可以維護(hù)10^3*10^3*10^3=10億條記錄。

實(shí)際情況中每個(gè)節(jié)點(diǎn)可能不能填充滿，因此在數(shù)據(jù)庫中，B+Tree的高度一般都在2~4層。MySQL的InnoDB存儲(chǔ)引擎在設(shè)計(jì)時(shí)是將根節(jié)點(diǎn)常駐內(nèi)存的，也就是說查找某一鍵值的行記錄時(shí)最多只需要1~3次磁盤I/O操作。

數(shù)據(jù)庫中的B+Tree索引可以分為聚集索引（clustered index）和輔助索引（secondary index）。上面的B+Tree示例圖在數(shù)據(jù)庫中的實(shí)現(xiàn)即為聚集索引，聚集索引的B+Tree中的葉子節(jié)點(diǎn)存放的是整張表的行記錄數(shù)據(jù)。輔助索引與聚集索引的區(qū)別在于輔助索引的葉子節(jié)點(diǎn)并不包含行記錄的全部數(shù)據(jù)，而是存儲(chǔ)相應(yīng)行數(shù)據(jù)的聚集索引鍵，即主鍵。當(dāng)通過輔助索引來查詢數(shù)據(jù)時(shí)，InnoDB存儲(chǔ)引擎會(huì)遍歷輔助索引找到主鍵，然后再通過主鍵在聚集索引中找到完整的行記錄數(shù)據(jù)。

以上就是動(dòng)力節(jié)點(diǎn)小編介紹的"MySQL索引原理"，希望對大家有幫助，想了解更多可查看MySQL教程。動(dòng)力節(jié)點(diǎn)在線學(xué)習(xí)教程，針對沒有任何Java基礎(chǔ)的讀者學(xué)習(xí),讓你從入門到精通,主要介紹了一些Java基礎(chǔ)的核心知識(shí)，讓同學(xué)們更好更方便的學(xué)習(xí)和了解Java編程，感興趣的同學(xué)可以關(guān)注一下。